| From: Kronos Vol. VIII No. 2 (Winter 1983) (PDF scan - parts I & II) | Home | www.Kronos-Press.com | Electricity in Space | Part I |
|
Copyright 1982 by the Estate of Ralph E. Juergens
*Editor's Note (Earl R. Milton): This paper was compiled by me from manuscripts and notes left uncompleted by the author at the time of his death. In reconstructing these documents, I have left intact as much of Juergens' original text as was consistent with their new form. Where necessary, short transitional statements have been inserted; these are printed in a distinctive type for ease of identification. Compiler's footnotes contain an alphabetic character while those of the author are purely numeric.
We have advanced the premise that the kinetic energy of the electrons in a stream converging upon the Sun is the source of the energy thrown off by solar radiation. With a cathode drop of 10 to the power 10 volts, each electron in the stream will arrive at the Sun with kinetic energy in the amount of 10 to the power 10 electron-volts. If these electrons were not moving close to the speed of light we would expect about 2.4 x 1035 electrons (originating in interstellar space not including those liberated by the ionization of solar atmospheric gases) to reach the Sun each second.
That the electrons impinge upon the Sun with velocities which are relativistic reduces the number of electrons which must arrive to supply the energy to power the Sun. Although the product of V (the cathode drop) times e (the electron charge) equals the kinetic energy of the current carriers, the acceleration of the galactic electrons within the solar discharge to velocities which approach the velocity of light causes effects not seen in more mundane discharges. From calculations simulating the behavior of electric currents produced by relativistic electrons it seems as if the discharge current delivered has a limit it does not continue to increase as the accelerating potential is raised to very large values. But an ever increasing potential can deliver linearly more energy to the discharge although no proportional increase occurs in the discharge current. The electrons which deliver the charge have become increasingly heavier than electrons at rest as their velocities asymptotically converged upon the velocity of light (see Appendix II). These relativistic electrons seemingly deliver "extra energy" to the electric discharge through their increased mass. ( 12a)
In spite of the enormous absolute potential we attribute to the solar environment,(13) there is no reason to expect interstellar space to be characterized by important potential gradients, at least not on a scale of star-to-star distances. Even if currents flow in the spiral arms of the galaxy as Bruce suggests, to a good approximation the potential should be uniform in all directions within a few light-years of the Sun (13a)
On this basis we could assume that most particles of matter indigenous to this region -- neutral atoms and molecules, positive ions, and electrons -- move in essentially random directions. The gas comprising these particles ought to behave as a thin, weakly ionized plasma.
It would follow, then, that the electrons eligible for capture by and participation in the solar discharge would be those whose random motions caused them to encounter the fringes of the electric field in the cathode drop of the discharge. The number of such electrons would be determined by the density of free electrons in space, the kinetic temperature of the plasma, and the size of the (spherical) region occupied by the solar cathode drop. But a calculation based on this approach would indicate that vast numbers of electrons should pour into the Sun.
Let us suppose that the effective velocity of a typical interstellar electron would be about 105 meters per second, corresponding to a kinetic temperature of a few hundred degrees Kelvin. From current estimates of the state of ionization of the interstellar gas, we might conclude that there should be as many as 50,000 free electrons per cubic meter.(14) The random electric current of these electrons then would be Ir = NeC/4, where N is the electron density per cubic meter, e is the electron charge in coulombs, and C is the average velocity of the electrons.(15) Using the given values, we find that the random electric current density should be about 2 x 10-10 amperes per square meter through a surface oriented in any given manner.
As we shall see later, the solar wind current noted at the Earth's orbit, when diluted by expansion to the postulated distance for the "edge" of cathode drop, is an order of magnitude below this estimate of the random electron current density (of 2 x 10-10 amperes per square meter). Can the discrepancy between electric theory and satellite observations be reconciled and understood in terms of other yet to be considered environmental factors -- such as the Sun's galactic classification and/or its location within the galaxy?
THE TWO POPULATIONS OF STARS
Since we are postulating that stars are powered by electric currents flowing from the stars to their surroundings, we should examine the stars of the galaxy and the nature of their galactic environments.
One of the most significant discoveries of the past few decades was that of Walter Baade of the Mount Wilson and Palomar staff. He was the first to recognize that the stars of the local galaxy fall into two general classes: Population I stars, of which the Sun is an example, are found mainly in the flattened disk of stars that dominate the outer part of the galaxy; they range in color from red to blue, with giant stars at both extremes, the blue ones being by far the brightest. Population II stars are found in globular clusters -- "satellite systems which surround our Milky Way, apparently hedging it about in all directions"(16) - and in great numbers in and about the galactic nucleus; the brightest stars of Population II are less brilliant than the blue giants of Population I and they are red in color, but brighter than the giant red stars of Population I.
It was soon noticed in studies of our own and other galaxies that Population I stars are present only in regions where there is dust. This dust is richer in metals than the typical interstellar gas, and the Population I stars seem to have a higher admixture of metals than those of Population II. Therefore, the consensus among astronomers is that the two populations represent two different age groups, the older stars of Population II having been formed from an earlier blend of ingredients, before metals were as abundant in the universe as they are now. The basic difference in the two populations is accepted to be one of metal content.
But the primary observational fact is this: "where there is no dust, there is no Population I."(17)
The Sun as a Population I star ought to be typical of its group. By examining its operation we might be able to draw some conclusions about the state of electrification of the dusty galactic disk. We start by considering the Sun surrounded by a sphere of space through which it draws energy from, and discharges current to, the galaxy.
The total electron current that can be drawn by the discharge is the product of the random current density and the surface area of the sphere occupied by the cathode drop. There is little to indicate how large this sphere might be, but in view of the enormity of the cathode drop it seems likely that the radius of the sphere would be large in terms of solar system dimensions. The mean distance of Pluto's orbit is 39.5 astronomical units, or about 6 x 1012 meters. We might guess that the cathode drop would reach to at least 1013 meters from the Sun, so that its spherical boundary would have a collecting surface area of somewhat more than 1027 square meters.
Such a surface could collect a current of interstellar electrons amounting to practically 1018 amperes twenty-five times greater than the total current that seems proper. And of course a larger sphere could collect an even greater current.
If the hypothesis is to be valid, we can only conclude that free electrons are extremely scarce in the interplanetary medium.
This, of course, is not in conflict with the ideas embodied in the suggested model of the galaxy; we postulated initially that free electrons must be overly abundant in the nucleus and positive ions overly abundant in the outer regions. Still, what we conceived was an imbalance in relative numbers, not an absence of one or the other type of particle in any absolute sense. If atomic matter is present, we must expect ionization to occur to some significant degree, and electrons must therefore be liberated in space. What happens to them'?
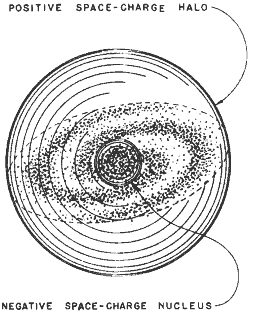 Figure 1. The Galaxy and Its Electric Space-Charge. A non-uniform distribution of space-charge in the galaxy at large could provide the driving potential for stellar electrical discharges. Such a galaxy has a spherical shell of positive space-charge at its outer limit and a uniform negative space-charge throughout the remaining volume of the galaxy. So modeled the galaxy provides a negative space-potential sufficient to sustain the solar discharge. |
One possible explanation for a dearth of free electrons in interstellar space suggests itself: The electrons may attach themselves to passing dust particles and thus become immobilized.(17a)
We have just speculated that cosmic dust may be filtering free electrons out of the interstellar gas and preventing them from flooding in upon the Sun. It is interesting to entertain the idea that the two populations of stars may differ fundamentally in the matter of current carriers in the cathode drop.
If, as suggested, the Sun and other Population I stars exist in an environment of electron scarcity, we must suppose that the discharge currents in the cathode-drop regions of these stars are carried predominantly by positive ions travelling outward. Population II stars, existing in regions where dust is not available to immobilize free electrons, may draw intense currents of electrons from their surroundings.(17b)
As a result of the galactic electrical structure proposed earlier,(18) the galaxy will be ion-rich at its periphery and electron-rich toward its center. The effect will produce a local space-charge which varies from place to place within the galaxy, as depicted in Fig. 1. The galaxy electrified can be viewed as a larger sphere of positive charges superposed upon a smaller sphere containing negative charges. The result is depicted at the top of Fig. 2. The electric potential associated with the spheres - separately and combined -- is shown at the bottom of Fig. 2 (18a)
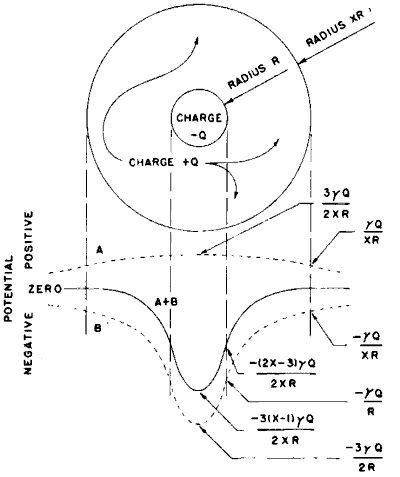 Figure 2. Hypothetical Charge Distribution Within the Galaxy. If the galaxy is seen as two superimposed spheres of opposite electric charge, the negative charge confined to a sphere of radius R and the positive charge within a larger sphere of radius XR, then an electric potential function can be computed across the galaxy. Above, the two charged spheres are shown, Below, are the potential curves for the positively charged-sphere (A), the negatively charged-sphere (B), and for the sum of the two spheres (A+B). The constant [gamma] has the value 9x109 in the meter-kilogram-second units. The charge (+Q, -Q) and the radii of the spheres containing them (R, XR) are presently undetermined. (See reference f for the numerical estimates of these parameters). |
The curvature of the potential distribution line in Fig. 2 is suggestive in this connection. Wherever such a curve is convex upward, one can immediately infer that the region represented is one of positive space charge. Where it is concave upward the curve marks a region of negative space charge. (We have of course postulated that the galactic halo harbors excess positive charge and the nucleus excess negative charge, and this is what the curve depicts.) It seems conceivable that. in the nucleus, electrons might be so abundant as to charge dust particles and power stars at the same time. And if dust is absent, as seems to be the case in some regions, all free electrons could be available to the stars.(18b)
The evidence is sparse, and we can only speculate as to its meaning, but in a tentative sort of way we may conclude that the two populations of stars present no immediate obstacles to the electric discharge hypothesis.
THE SOLAR DISCHARGE
We can picture the solar system as a region in space dominated by a continuous electric discharge, the Sun. To do so we start with the idea of an electrical cavity, a sort of "flaw" in the fabric of the Milky Way Galaxy. From our point of view this cavity has almost incomprehensibly grand proportions, but - from the viewpoint of its scale and importance in the galaxy -- it is a minor, localized disturbance. At the center of this electrical "flaw" is a rather ordinary star, which is induced to absorb great quantities of electrons and spew forth in all directions protons, positive ions, and electromagnetic radiations of every kind.*
[*For a complete discussion of the situation, see the editor's footnote at the bottom of p. 8 in KRONOS VIII:I.]
There is a higher electric potential near the Sun than in the galactic medium; hence the Sun accepts currents of galactic electrons and functions as an anode. The wall of the imaginary cavity therefore becomes the "emitter" of electrons, or the cathode.
Instruments carried into space have shown that there is a "solar wind" of protons and other positive ions blowing outward continuously from the Sun. Thus we must assume that the total discharge current is carried by particles of opposite charge moving in opposite directions - electrons toward the Sun, and protons away from the Sun. If we assume that the electrons in the undisturbed galactic medium move - for all practical purposes, in random directions -- it follows that, at the cavity "wall", the current must be carried almost entirely by protons. At the surface of the Sun, on the other hand, we may assume that the protons start to move outward with almost negligible velocity, so that the current into the anode is carried entirely by electrons. From these considerations we shall be able to arrive at some sort of estimate of the size of the hypothetical discharge cavity.
In form, the discharge would seem closely analogous to a coronalike discharge from a positive point. Cobine points out, however, that the term corona, by convention, is applied primarily to discharges at relatively high gas pressures in the terrestrial environment.(19) In the Sun's atmosphere, gas pressures are everywhere low by earthly standards, so it will be convenient to discuss our model in terms usually applied to low pressure glow discharges, bearing in mind, however, the spherical geometry imposed by our first postulate.
Still, as we shall see, there are compelling similarities between phenomena observed in corona discharges and phenomena observed in the atmosphere of the Sun. In any case, the corona discharge is acknowledged to be a form of glow discharge, differing principally in geometry from the glow discharges that are studied in cylindrical discharge tubes. Thus, it is a matter of no great concern that we choose to analyze the solar discharge in glow discharge terms rather than in terms of corona discharges.
At the outset we should note certain factors that must tend to introduce complications and, hence, invalidate certain analogies to varying degrees. Perhaps the most important of these is the gravitational field of the Sun, especially insofar as it affects gas densities in different regions of the postulated discharge.
For reasons that will soon become clear. the postulated discharge -- though focussed on a central solar anode - would appear to embrace a vast region of space, most of it devoted to cathode mechanisms. The solar corona, and its extension through interplanetary space and beyond, finds an analog in the "negative glow" region of a glow discharge. The chromosphere we shall interpret as the inner limit of this negative glow. Only the photosphere, at the inner limit of the vast discharge cavity, will be assigned an anode function in this model.
The focus of the discharge is the Sun itself, an anode serving as both a source for positive and a sink for negative charge carriers. The flow of such carriers between the interstellar medium and the Sun constitutes the electric current that powers the Sun.
As already indicated, an implicit assumption of the solar-discharge hypothesis is that galactic electrons flow toward the Sun in a stream moving counter to that of the solar protons. This is clearly incompatible with Parker's hypothesis(20) -- the source of the term "solar wind". In his view, which is widely accepted, solar plasma comprising both protons and electrons moves outward in an unending stream from the Sun. Up to now, however, with Parker's assumption implicit in their design, most deep-space probes have sampled only the proton flux, and the drift of electrons has been assumed to correspond to the drift of positive ions.(21)
The sunward currents of electrons that are all-important to the present hypothesis might be investigated with suitably designed space probes, especially since preliminary calculations (see below) suggest that these currents in the vicinity of the Earth would be carried by electrons moving at (very nearly) the velocity of light. Detection may be made difficult, however, by the fact that such fast electrons quickly charge up the detecting instruments to the point where they repel electron currents. Probes of presently feasible proportions may be unable to carry apparatus sufficient to maintain suitable potentials on electron detecting devices, such as the Faraday cup.
The surface of a sphere with a radius equal to that of the Earth's orbit is 2.8 x 1023 square meters. An electron current of 4 x 1016 amperes crossing through such a total area with uniform distribution yields a current density of 1.4 x 10-7 amperes per square meter, a value that can be achieved if the interplanetary medium contains something less than 3,000 relativistic electrons per cubic meter streaming toward the Sun.
Satellite measurements give an electron population in the local plasma of 9 to 11 per cubic centimeter,(22) which amounts to 9 to 11 million per cubic meter. (The discharge hypothesis suggests that most of these are secondary electrons generated by the ionization of solar gases.)
On the average, measurements show that most of these detected electrons are moving neither inward nor outward. Parker's model requires that a like number of electrons and ions drift outward, constituting the electrically neutral solar wind. Here, we require that an inward flux of 3000 relativistic electrons per cubic meter pervades the background of 9 to 11 million electrons per cubic meter which occupy, but do not flow through, the space between the planets of the solar system.
On this basis, we are at least partially justified in supposing that the negative glow of the solar discharge cannot be located outside the Sun's atmosphere. Since the negative glow is the first true plasma region to be encountered as we proceed from the cathode of a glow discharge toward the anode, the interplanetary plasma may be tentatively assigned this role without straining the self-consistency in the model.(23)
Thus it would appear that, if but one in about every 3,000 electrons near the Earth turned out to be a current carrier moving at almost the speed of light toward the Sun, the power delivered would be enough to keep the Sun "burning" at its present rate. This seems a rather subtle stream but it would suffice to power the Sun.
Appendix II: Relativistic Electrons and Protons
The theory of relativity says that the maximum possible velocity for transporting matter or energy is the velocity of light, c = 2.998 x 108 m/sec. Under ordinary (low potential) conditions, the work done on an electron charge e that is accelerated through a potential drop of V volts is Ve. In empty space where the electron suffers no collisions, this work is converted entirely into kinetic energy, or energy of motion at velocity v amounting to ½mv2. Here m is the mass of the electron. The equation that expresses these facts is Ve = ½mv2. From this, we see that the velocity of the electron is given by v = (2 Ve/m)½ . If we try to apply this equation to the extremely high voltages, however, we run afoul of the theory of relativity; for example, a voltage drop V of the order of 106 volts would yield a velocity for electrons far in excess of c.
Relativity theory gets around this sort of problem by saying that as a particle approaches the velocity of light its effective mass, or inertia, increases. As electrons are accelerated to ever higher energies, the velocities slowly approach ever closer to that of light, while the effective electron mass goes up sharply. Theory and experiment indicate that the mass of an electron me travelling at velocity v exceeds the electron rest mass (me)O by a factor of 1/(1-v2 /C2)½ ; that is:
| 1 | |
| me = (me)o | --------------- |
| 1/(1-v2 /C2)½ |
and, for protons travelling at relativistic velocities.
| 1 | |
| mp = (mp)o | --------------- |
| 1/(1-v2 /C2)½ |
The kinetic energy of a particle is the difference between its energy at rest with mass mo and its energy when in motion with mass m and velocity v. The classical equation for kinetic energy, Ve = ½mv2, is actually only an approximation that is valid at low (non-relativistic) velocities. For high velocities the kinetic-energy equation must be modified to take into account the relativistic increase in particle mass. The result is Einstein's law:
| 1 | ||
| Ve = (mo) c2 | --------------- | - 1 |
| 1/(1-v2 /C2)½ |
It can be shown that for very low values of v/c - which is to say for non-relativistic velocities - Einstein's general equation yields results practically identical with the classical or Newtonian equation.
It is useful and instructive to portray the implications of the kinetic energy equation graphically. We can do this by inserting arbitrary values for the ratio v/c into the equation, calculating the voltage drops V required to yield these ratios for particles of different rest masses, and plotting the results as a series of curves. Such curves for electrons and protons are shown in Fig. 4. The dashed lines labelled A and B show how curves derived from the classical equation of kinetic energy diverge from reality at high velocities.
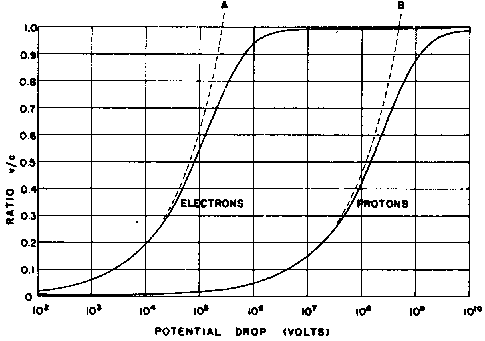 Figure 4. Velocities of Electrons and Protons Accelerated Through Great Electrical Potential Differences. The dotted curves labeled A and B are the velocity curves calculated using Classical theory. The solid curves include the correction for increased mass with increasing velocity in accordance with the Special Theory of Relativity. |
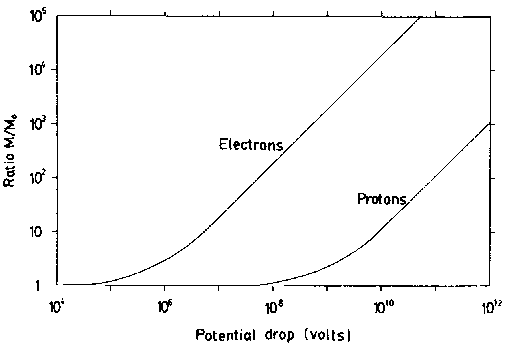 Figure 5. Mass Enhancement for Relativistic Electrons and Protons. When accelerated through great electric potential differences electrons and protons asymptotically converge upon the speed of light in vacuo. Their greatest energies make them appear to have an enhanced mass (M) in comparison to their mass at rest (Mo) The ratio of their mass in motion to their mass at rest increases measurably with increasing energies above a specific "threshold" for each particle. |
Inspection of the kinetic-energy equation indicates that curves of the type shown in Fig. 4 for any two kinds of charged particle will be displaced from one another on the potential-drop scale by an amount equal to the overall ratio between the individual mass-to-charge ratios. Thus, whereas an electron accelerated through a drop of 105 volts achieves a velocity of about 0.55c, a proton - carrying the same charge, but 1836 times the rest mass of the electron - requires a voltage drop of 1.84 x 108 volts to reach a velocity of 0.55c.
Additional relevant (and revealing) curves can be drawn by plotting the ratios m/mO of relativistic mass to rest mass for both electrons and protons against the voltage drops required to yield such ratios. Fig. 5 shows such curves for these two types of particle.
Both curves, of course, begin asymptotic to a horizontal line at
m/mo= l, for the relativistic mass can never be less than the rest mass. The electron and proton curves approach being parallel at the upper limit of the indicated voltage scale: thereafter they differ by 1836; the electron mass has increased 1836 fold relative to the proton mass for the same energy.
Now, let us again use secondary subscript symbols to differentiate between electrons and protons. Thus me and mp will stand for the relativistic masses, respectively, and (mo)e and (mo)p will designate their rest masses.
If we read off the curves of Fig. 5 at different values of V the corresponding values of (m/mo)e and (m/mo)p, we can tabulate them as follows:
| V
(volts) |
(m/mo)e | (m/mo)p | mp/me= 1836 | mp/me |
| (mp/me)o | ||||
| 104 | 1.0 | 1.0 | 1836 | |
| 105 | 1.2 | 1.0 | 1530 | |
| 106 | 2.8 | 1.0 | 660 | |
| 107 | 18.6 | 1.0 | 99 | |
| 108 | 190 | 1.1 | 10.7 | |
| 109 | 1900 | 2.1 | 2.03 | |
| 1010 | 19000 | 11.5 | 1.11 | |
| 1011 | 190000 | 110 | 1.06 | |
Plotting these results (Fig. 6) we get a very interesting curve. As we would expect, for low voltage drops, the ratio between the proton and electron masses is the same as that between their rest masses. As we move upward to voltage drops where electrons, but not protons increase steeply in relativistic mass, the ratio of the effective masses starts to decrease rapidly. But when we consider voltage drops of such magnitude that the proton effective mass climbs steeply, we find that the ratio of the effective masses of electrons as against protons traces a reversal of curvature and ultimately approaches a value of unity. Infinite voltage drops produce infinite relativistic masses for both types of particle. The limiting ratio of their masses (mp/me) should be unity. But it is something of a surprise to find that same ratio achieves a value that is practically unity with a drop of only 1010 volts, the same value that we estimated for the cathode drop associated with the solar discharge! Could this just be a coincidence?
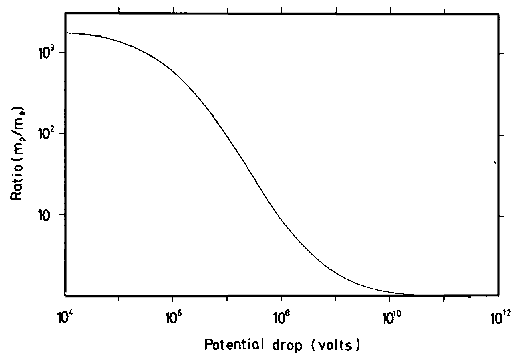
Figure 6. Comparison of Electron and Proton Masses at High Energy. At rest protons are more massive than electrons by a factor of 1836. Electrons moving with velocities which approach the speed of light becomes sufficiently "heavier" so their mass approaches that of slower moving protons having the same energy as the electrons. |
Appendix III: Relativistic Electric Currents
by George Robert Talbott and Earl R. Milton
We wish to understand the current produced by electric potential differences on a galactic scale. We have postulated that galactic potentials can produce electric currents where the carriers (especially when they are electrons) may reach velocities which approach the velocity of light (see Fig. 7).
An electric current is the net charge flowing past a point (or through some small area) over an interval of time. It can be expressed in terms of the number (n) of electron-charges (e) flowing:
n e =I t (1)
where I is the current (in charges per second) and t is the time in which those charges flow past some point.
It is also meaningful to know the number of charges along any unit of space, which we shall designate as h (charges per meter). With h an expression can be produced relating the velocity of the current carrier (v) to the current (I)
I = h e v (2)
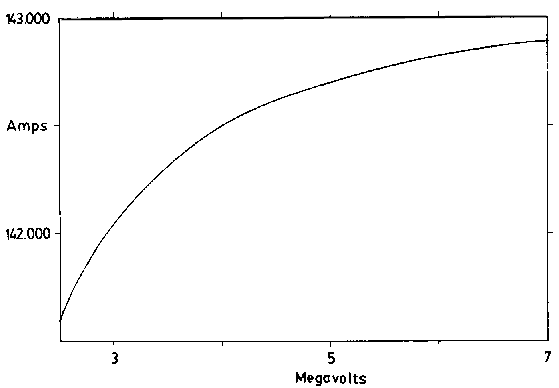 Figure 7. Current Produced by Field Accelerated Charged Particles. As the velocity of accelerating electrons approaches the speed of light, the current change produced by further acceleration decreases producing a current "limit" for the potential field which is producing the current. |
Now we may relate the current flowing to the potential difference using the energy relation
V e = ½ m v2 (3)
where m is the effective mass of the current carriers, v is their velocities, and V is the accelerating potential.
For a relativistic velocity this becomes
| mo | ||
| V e = ½ | --------------- | v2 (4) |
| 1/(1-v2 /c2)½ |
in which mo is the rest mass of the carriers, v is their velocity, and c is the velocity of light in a vacuum. Introducing current for the charge and velocity terms [using (1) and (2)] the equation becomes
| Vt | mo | I |
| -- = ½ | ------------- | ------- |
| n | 1/(1-v2 /c2)½ | h2 e2 |
or
| V = | { | mo n | } | I (5) |
| ---------------- | ||||
| 2tη2e2 (1-ν2/c2)½ |
an equation which has the simple form of Ohm's law (V=RI) but is quite complex since both the h and v factors within the "resistance" term affect the current. Notwithstanding a galactic resistance term can be visualized from the coefficient
| R = | mo n |
| ---------------- | |
| 2tη2e2 (1-ν2/c2)½ |
As the velocity of the current carriers approaches c the circuit becomes infinitely more resistive in a complex way. The resulting galactive resistance allows self-limiting cosmic discharges to occur producing observed stellar luminosities.
Perhaps more informative is the re-expression of the energy relationship (4) in terms of the potential
| mo c | v2 | ||
| V = | ----- | ----------- | (6) |
| 2e | (c2 - v2)½ |
which can be evaluated by inserting various electron velocities. The accompanying currents can be obtained from equation (2). Their quotient gives the galactic resistance for the cosmic discharge circuit.
An alternative means of demonstrating the relativistic increase in electrical resistance is to rearrange equation (4) as follows:
| V = | { | 2(b4/c4 + b2)½ - b2/c2 | } | ½ | (7) |
where b = Ve/mo. The velocity so found can, by equation (2), be converted to an electrical current. The ratio of the potential to the velocity-deduced current is the relativistic resistance. This will be seen to rise with the velocity, just as expressed in the other equations. The alternative derivation is interesting, and allows an independent approach in which potential is stipulated first, and then the consequences are deduced.
NOTES AND REFERENCES