| From: Kronos Vol. IV No. 4 (Summer 1979) (PDF scan | Home | www.kronos-press.com | Electricity in Space |
|
Copyright © 1979 by R. E. Juergens
We cannot see inside the Sun. Although the interior is unquestionably ablaze with radiation, we can view it only indirectly; theory alone can light the way.
On the outside, however, fairly direct observations can be relied upon for clues to the workings of our local star. If, as is almost universally accepted, the Sun is a thermonuclear engine whose primary concern on the outside is the radiation of excess energy liberated from matter deep in its core, observations of the visible regions, particularly the brilliantly luminous shell that masks the interior, ought to suggest as much. We have no reason to suspect that nature in the physical universe goes out of its way to camouflage its activities.
Suppose, then, that we put aside our preconceptions of whatever may be happening within the Sun and look to the visible evidence. As we emerge from the unseeable depths into the light of the solar atmosphere, the first region we come to is the photosphere - a white-hot envelope of hot plasma that gives off practically all the radiant energy we think of as sunshine.
Here is where the Sun could well be expected to "end," if indeed the dissipation of internally generated energy were basic to the maintenance of its mechanical equilibrium, as the accepted theory claims. Yet the photosphere in no way ends the Sun; rather, it is more truly just the beginning, or base, of an atmosphere of enormous reach and baffling complexity that seems perversely contrived to hinder more than help radiant energy to escape.
I
The term photosphere goes back to the time of William Herschel, possibly the most influential astronomer of the early nineteenth century. He believed that the Sun has a cool, solid surface, abounding with life. The Sun's radiation, he taught, originates in a brilliantly luminous layer of clouds at the top of its atmosphere, and sunspots are clearings through which the lower regions and the surface may occasionally be glimpsed.
Today such notions seem rather quaint. But because of Herschel's otherwise well-earned reputation as a great astronomer, his ideas about the Sun persisted for many years after his death.
J. Schroeter, a German amateur astronomer and a devoted follower of Herschel, is credited with coining the word "photosphere" as a name for the Sun's envelope of luminous clouds. And during the extended tenure of Herschel's image of the Sun the term gained universal acceptance.
One of the strangest aspects of the photosphere is its lumpy structure. Under conditions of good astronomical "seeing," instead of presenting the surface of uniform brightness that might be expected, the photosphere shows up as discrete patches of high luminosity in a field of lesser luminosity. The effect is not unlike looking down on closely packed, fluffy clouds.
This was already known in the days of Herschel and Schroeter and was clearly the inspiration for the concept they espoused.
On the basis of modern photographic observations and what is now understood concerning photospheric temperatures, it may be said that the Sun's bright envelope consists almost entirely of distinctly formed blobs of hot plasma.
For some years this puzzling, composite quality of the photosphere was referred to as its "rice-grain structure". From this evolved the more prosaic terms granulation - used with reference to the overall graininess - and granule - the designation for an individual "rice grain" or puff of plasma. So, now one speaks of a photosphere that exhibits granulation in its texture, or consists of millions of individual granules.
Only a few decades ago knowledge of photospheric granulation was still rather sketchy. It was known that granules average perhaps 1000 kilometers in diameter and that they come and go on the solar surface with lifetimes measured in minutes. Sometimes budding granules would seem to push up from below, shouldering aside older ones or replacing others that had expired. New granules frequently bloomed with vertical motions greater than 1000 kilometers per hour, but lateral motions with respect to the background field were much slower and were seldom observed.(1)
In any case, the effects of turbulence in the Earth's atmosphere made seeing difficult. The dimensions of granules put them at the lower limits of resolution for observation with earthbound telescopes.
A major advance in the study of granulation came with the success of Project Stratoscope, an effort mounted by Martin Schwarzschild and several co-workers at Princeton University in the late 1950's. In this program, telescopes were carried into the stratosphere by balloons. At such heights, some 25 kilometers above sea level, the Earth's thin atmosphere causes little blurring of telescopic images. The stratoscope flights of 1959 yielded a number of excellent photographs of solar granulation and sunspots.
In the early 1960's, investigators at Sacramento Peak Observatory in New Mexico obtained a series of high-quality images of the photosphere on motion-picture film. They exposed consecutive frames at intervals of several seconds, producing a time-lapse "movie" of granule activity. Projection of their film showed that "the lifetime of an individual granule is very hard to define. Several small granules may join to form a large one, which grows in size and intensity until its length may exceed 2,000 kilometers. Then the large granule splits into smaller ones and diminishes in intensity. Such fragments unite with adjacent small granules to form another large one, which also grows and brightens until it splits about eight minutes later . . ."(2)
At one time, on the basis of difficult visual observations, it was believed that bright granules covering no more than one-fifth of the solar surface radiated three-fourths of the Sun's light. Later estimates gave the granules and the darker spaces between them approximately equal areas on the total solar surface. But the stratoscope pictures showed that most of the surface is covered with granules, and that the darker areas consist primarily of narrow gaps between granules.(3) A few years ago, estimates of the total number of granules present at a given moment ranged to about two million. After studying the stratoscope photos, however, O. Namba and W. Diemel concluded that the figure should be increased to about six million.(4)
But why should the surface of the Sun be lumpy? Ought not a star like the Sun, supposedly bent on divesting itself of excess energy liberated deep in its interior, be able to compose itself and form a smooth surface for a steady output of radiation?
Herschel, as we have seen, believed the anomalous lumps to be clouds. The modern belief - less fanciful, perhaps, but no less speculative - is that the granules are "the changing tops of convection currents bringing light and heat from an unstable layer beneath. The enormous flood of radiant energy generated within the sun pours forth at last into space".(5)
M. Minnaert, the late director of Utrecht Observatory in Holland and a leading solar physicist, reflected the views of perhaps 99 percent of his colleagues when he once stated that "the study of the granulation demonstrates that some photospheric layers at least are in constant turbulent motion" and that this is evidence of convection.(6)
J. A. Hynek, as director of Dearborn University at Northwestern University, spelled it all out for the non-specialist: "Most astronomers are now fairly certain that these bright cells are the tops of columns of hot gases being rapidly transported from 'subsolarian' depths to the surface. As they cool, these columns of hot gases begin to sink. And, as an effect of cooling, they lose their brilliance, appear dark by contrast to hot ascending columns . . . It seems that the sun's surface is like a patchwork of blindingly brilliant geysers, each 100 thousand square miles in area, violently erupting every few minutes."(7)
Mysteriously, however, the granules fail dismally in living up to such billings. True enough, observers report rapid upward motions and the speedy growth and decay of granules. But the motions are nevertheless orderly, the growth cycles disturbingly non-violent. Such effects hardly qualify for characterization in terms of turbulent eruption.
Though the point is seldom conceded, the established theory of stellar energy is embarrassed by the mild behavior of the Sun's photospheric granules.
Many years ago, F. R. Moulton, an astronomer who never doubted that the energy of the Sun came from within its body, remarked that the photosphere "must be a region of violent convective currents, for heat could not be conducted to the surface anywhere nearly so rapidly as it is radiated away".(8) However, were granulation really due to turbulent convection, we should expect the brighter areas, where the hotter gases well upward, to exhibit entirely random forms. Roughly hemispherical forms might well be abundant, but for the most part the chaotic turbulence should heave up masses of hot, bright gas with disordered, highly contorted outlines. Yet observed granules appear highly ordered, giving every appearance of being distinct "nodules" (Moulton) distorted only by crowding or by merging and splitting tendencies.
Furthermore, were the darker regions of the photosphere simply areas of turbulent subsidence, where gases cooled by radiation fell back toward the interior to be reheated, we should expect them to have equally chaotic forms. In reality, however, "there is a striking topological asymmetry between the brighter-than-average and darker-than-average areas"(9); there is not the slightest resemblance between their forms, and there is not even approximately equal sharing of the available surface area between them. The darker areas "appear as networks of lanes or 'canals' running between the bright granules" (10)
The idea of turbulent convection delivering endless loads of energy upward from the unseen depths of the Sun conflicts not only with the ordered structure of the photosphere but also with the observable integrity of individual granules. The nodules of plasma appear, endure for some minutes, then fade away. As already noted, there is evidence that fading granules divide, and that some of their fragments merge with others to bloom again. But among full-blown, individual granules there is little indication of the violent mixing and roiling to be expected in a homogeneous fluid stirred by strong convection currents.
Each granule seems to fulfill a localized function; when its job is done, it retires from the scene quite unobtrusively by simply fading, splitting into lesser components, or subsiding. Yet during most of its lifetime it behaves as if it were bound and bounded by forces or conditions presenting effective barriers to lateral motion or diffusion.
The peculiar mode of rotation of the photosphere also argues against the idea of turbulent convection. Near the solar equator the period of rotation is about 25 days. At higher latitudes the period lengthens, and near the poles identifiable photospheric features take about 35 days for a complete turn. Long ago it was remarked that, if strong convection were actually present, "it is not clear that these vertical currents might not rather speedily bring about uniformity of rotation''.(11)
Considerations like these led astrophysicists to attempt explanations for granulation in terms of an effect known as non-stationary convection.
When a very thin layer of molten wax, for example, is kept heated in a flat pan over a low flame, the surface of the liquid breaks up into well-defined polygons and takes on the appearance of a mosaic pattern. The individual polygons are known as Benard cells, after the scientist who first reported the effect at the turn of the century. The phenomenon giving rise to the cells is called stationary convection.
(In the mid-1950's, M. Block found that the cells "disappeared when a surface-active layer of molecular thickness was spread on the liquid. Evidently they were caused by the temperature-dependence of the surface tension". "Benard's beautifully regular 'convection cells' resulted from capillarity, and not from convection . . .". - thus reports E. Orowan.(12) However, if convection is not responsible for Benard cells, the fact does not seem to have come to the attention of solar physicists.)
If the depth of the molten wax is moderately increased, the Benard cells assume less regular forms, and the term non-stationary convection is applied. The overall appearance of the liquid surface in this state is reminiscent of photospheric granulation in the best photographs.
Quite naturally, when this phenomenon came to the attention of astronomers, it was quickly seized upon as a possible explanation for photospheric granulation. Some were carried away with enthusiasm when Schwarzschild's Project Stratoscope photos first became available. For example, G. Abetti insisted that "An interesting fact has thus been established from the photographs: the appearance of the solar surface is due to effects of 'non-stationary' convection''.(13) Others, such as J. C. Brandt, were rather less dogmatic: "By analogy with classical studies of convection, we expect a cellular flow pattern say with hot gases rising in the middle of the cell and the cool gases sinking at the cell boundary. The solar granulation . . . is apparently the result of the penetration of these cellular motions into the photosphere. "(14)
At this point we are prompted to ask whether, by analogy or otherwise, we should really "expect a cellular flow pattern" to be evident in the solar photosphere.
The question of applying classical studies of convection to the photosphere comes down to questioning the propriety of equating an effect observed in molten wax or some other liquid with another observed in the tenuous plasma of the Sun's lower atmosphere. According to the principles of the physics of fluids, this is appropriate if certain relevant matters are taken into consideration.
One of these matters is the well known Reynolds number, a dimensionless measure that combines several physical parameters and pinpoints conditions under which a moving fluid will behave this way or that way. The number is essentially a ratio between forces tending to accelerate a fluid medium and viscous forces that resist such acceleration. Under given conditions, motions in one fluid - liquid, gas, or plasma - will be unlike those in another fluid unless their respective Reynolds numbers are approximately the same.
When the Reynolds number of any fluid exceeds a critical value, flow in that fluid due to convection or any other accelerating force will be turbulent and highly complex.
Minnaert once published an analysis of photospheric behavior in terms of the Reynolds number. He found the critical value to lie near 10³. The actual Reynolds number of the photosphere, as calculated from observable characteristics of the plasma, turned out to be in excess of1011, which is to say, at least 100 billion times greater than the critical value. Clearly, then, any convective motion in the photosphere should be violently turbulent and highly disordered, as Minnaert indeed pointed out.(15)
Practically in his next breath, however, Minnaert asserted that "The variable forms of the granules and their short lifetimes are evidence of nonstationary convection."
Such an abrupt about-face is startling. Apparently Minnaert, himself, was disquieted; he immediately set out to minimize his non sequitur by suggesting ways and means for disregarding the classical theory of turbulence to make things come out right for the photosphere.(16)
A second matter to be weighed in judging whether we should expect cellular-flow patterns in the photosphere is the Rayleigh number. This is a criterion developed specifically in connection with Benard's observations by Lord Rayleigh, H. Jeffreys, and others.(17) It takes into consideration other variables, including temperature gradients, depths of convective layers, and density gradients. Again the number has a critical value beyond which instability and turbulence set in.
And again the photosphere is a disappointment.
"If one calculates the Rayleigh number appropriate to the bottom of the solar photosphere, one finds that it exceeds the critical value by five powers of ten and therefore the solar granulation should on this basis be an entirely random phenomenon. The fact that the observed granules have a pronounced cellular structure and a bright-dark asymmetry has not yet been explained by theory.''(18)
Many facile assertions to the contrary, it becomes increasingly obvious that photospheric granulation is explainable in terms of convection only if we disregard what we know about convection. Surely the cellular structure is not to be expected.
It bears mentioning, too, that non-stationary convection in the laboratory takes place throughout the depth of the experimental medium. In assigning a like effect to the photosphere, we must suppose convective transport of energy suddenly to cease in mid medium and give way to transport of energy by radiation; as far as can be determined, the composition of the photospheric plasma is exactly the same as that of the overlying medium. How might we account for a mid-medium cessation of convection?
The conventional response on this point is less than satisfying. It harks back to the seeming reason why one looks for convection in the first place. And it has to do with the fact that the photosphere blocks our view into the interior of the Sun.
As the argument goes, energy liberated through thermonuclear reactions deep inside the Sun struggles to escape. For much of the distance to the surface the escape route accommodates transport in the form of radiant energy, though not without difficulty. At some depth below the surface, this path is blocked; the gases become opaque, and radiation cannot get through. An unstable condition results.
At this depth, conveniently enough, the gases are dense enough to handle the energy traffic convectively. They absorb the radiant energy until they become hot enough and buoyant enough to start rising like bubbles toward the surface, carrying their cargoes of energy upward by their bulk motions. At the surface, necessarily defined as that level where transparency is re-established, the rising cells of hot gas unload by radiating their energy into space. They cool, increasing in density in the process, then plunge back into the depths to complete the transport cycle.
Common sense argues that it is safe to say, with Zirin, that "the transport of energy will proceed by whichever process [radiation or convection] moves it most quickly''.(19) Where opacity stems the flow of radiant energy, heat will build up and steepen the temperature gradient in the medium until convection sets in. And when hot gases convecting upward break out into "the blue," they must surely radiate, cool, and stop convecting.
But we must recognize, also, that in the photosphere the gas density diminishes rapidly with height. Under such conditions, even if orderly convection (non-stationary convection) might be entertained in connection with the deeper layers, turbulent convection must certainly take over at the top of the pile, where the values of the Reynolds and Rayleigh numbers soar. Yet the Sun gives no evidence of this. The granules, obviously radiating fiercely, are there, and then they are not.
So the idea of thermal convection as the explanation for granulation in the photosphere - a concept that at first seemed handsomely supported by a resemblance between granules and blocky cells in molten wax - fares rather badly when subjected to scrutiny. Nevertheless, so compelling is the conviction that the Sun generates its own energy that such practical difficulties are generally disregarded. The consensus has it that convection there must be, and therefore photospheric granulation must somehow be a manifestation of the process.
Given that energy flows outward through the upper parts of the Sun, it would be foolhardy to deny convection a role in regions where solar gases are opaque, as in the photosphere. We have seen, however, that the observable structure of the photosphere in no way lends support to the premise; assigning a convective function to the relatively passive granules is possible only if established physical principles are disregarded.
It seems only reasonable, then, to question the theory that leads us to seek evidence of convection in the body of the Sun.
II
The structure of the solar atmosphere strongly suggests that the Sun is fueled not from within but from without, and that the energy-delivery mechanism is an electric discharge.(20) Can photospheric granulation find an acceptable explanation in terms of such a premise?
Perhaps so.
The fundamental sameness of the media inside and outside a photospheric granule is a fact to be reckoned with and may indeed be an important clue. There is a rather pronounced step, both in gas density and in luminosity, between the matter constituting a granule and that in which the granule forms and spends its brief lifetime.(21) Yet, as we have already noted, the stuff of the granule is essentially the same as that of its surroundings; both media are largely hydrogen gas, ionized to the plasma state.
On any appraisal, then, a granule may be viewed as a relatively dense, highly luminous, secondary plasma that springs into being in the embrace of a thinner, less luminous, primary plasma. Where on earth might such a phenomenon be observed?
The electric-sun hypothesis assigns the solar body the role of anode - that of the higher-potential electrode - in a cosmical electric discharge. Considering this, and recognizing granules as cells of secondary plasma, we are led directly to ask whether the granules might not be akin to certain highly luminous tufts of discharge plasma variously described in the literature as anode glows, anode tufts, and anode arcs.
Irving Langmuir, who was one of the first to study this phenomenon, used the term anode glow. This is aptly descriptive, but it introduces a measure of confusion; the same term is applied to the formation of a continuous, glowing "skin" or "film" of plasma-like sheathing on an anode surface. Later writers have avoided using the word glow in connection with the discrete blobs of glowing plasma which, as we shall see, closely resemble photospheric granules in form, behavior, and many other qualities, although certainly not in scale.
In his research reports and general reviews of the early work in plasma physics at the General Electric Research Laboratory, Langmuir frequently described these luminous objects, which spring into being under suitable conditions and appear to float just above an anode surface. He described their forms as "globular or semispherical," "more or less spherical," and like a "ball". Their luminosity he characterized as "several times more luminous than the surrounding" plasma, and as "intense". And he emphasized the sharpness of their outlines, at the same time acknowledging that they were bounded by transition zones and not by true surfaces.(22)
Already the reader will perceive several similarities between these anode tufts, as we shall call them, and photospheric granules.
Langmuir explained that anode tufts appear at localized points of electric breakdown in an anode sheath. When the electric current to the anode becomes excessive, breakdown - further ionization of the medium - takes place, and "a second plasma will form within the first".
To follow Langmuir's argument, we must first recall that the particles of matter in a discharge plasma have two kinds of motion. First are the random (thermal) motions reflected in the "temperatures" of the several populations of particles: electrons, positive ions (including bare atomic nuclei), and electrically neutral particles (atoms and molecules) all rush around every which way at different speeds. Typically, electrons, the least massive of all these particles, have the highest random velocities.
In addition to the thermal motions, and superimposed upon them, there are drift motions among the electrically charged particles (electrons and positive ions) in response to weak electric fields that pervade the plasma regions of any electric discharge. (Magnetic fields present in the plasma also affect the motions of charged particles, but this need not concern us in the present discussion.) The electrons, speeding in all directions, "sense" these electric fields of the discharge and tend to drift toward the anode. Positive ions tend to drift in the opposite direction, away from the anode and toward the cathode. This combined drift of negative charges in one direction and positive charges in the other direction constitutes a drift current - the entire electric current of the discharge through the plasma.
To maintain a steady discharge, the anode must collect an uninterrupted stream of electrons whose electric current, or flow of charge per unit time, equals the total drift current in the full cross section of the discharge plasma. (For purposes of the present hypothesis, the discharge "cross-section" may be thought of as a closed, spherical surface in space, outside the Sun at some distance beyond the reach of distinctly "anode" phenomena; say, arbitrarily, at perhaps a few solar radii from the photosphere.)
Now, the random motions of the plasma electrons are usually much more energetic (faster) than their drift motions. In any case, they complicate matters for an anode bent on maintaining a stable discharge.
Suppose, for example, that the area of the anode surface equalled the plasma cross-section. (For the Sun, this would mean that the interplanetary plasma extended all the way to the solar "surface".) If the anode were in direct contact with the plasma, it would tend to receive not only the electron drift current but also a random current delivered by those electrons whose thermal motions within the plasma happened to be toward the anode at a given instant. With the electron random current exceeding the drift-current component due to the positive ions (moving in the opposite direction), the total current collected by the anode would be more than the discharge could sustain, and an instability would result. (This suggests, perhaps, one possible explanation for the highly variable behavior of certain stars.)
The remedy is for the anode to disengage itself from the plasma. Initially, it accepts a certain number of excess electrons and takes on a slightly negative charge (relative to the plasma) - a slightly lower relative potential - which repels all but the most energetic of the electrons approaching thereafter. The anode adjusts its potential to a value that permits the further arrival of only enough electrons to deliver a current equalling that carried by the discharge plasma. Rejected electrons return to the plasma, leaving behind a thin sheath of positive space charge - a region "overpopulated" by positive ions - between the plasma and the anode surface.
Due to this adjustment, the anode electric potential is now somewhat lower than that of the plasma being held at bay. The region that Langmuir named the sheath bridges the distance between anode and plasma, as well as the difference in potential between them. The sheath thus "contains" (limits) the electric field due to the excess negative charge on the anode. In other words, the positive space charge of the sheath counterbalances the excess negative charge taken on by the anode in making its adjustment.
Now, if the anode had less surface area than one exposed to the full cross-section of the plasma, it would still have to collect the same total electric current. This would mean that the current density at the anode surface would have to exceed that in the discharge plasma. The anode would have to collect more of the random current to make up the difference. In this case, the anode could maintain stability by giving up some electrons and increasing its relative potential, adjusting its positive-ion space-charge sheath to span a lesser potential drop (difference) between its surface and the outer, discharge plasma.
Were the anode further reduced in size, to the point where the stable-discharge current could be collected only if all approaching electrons - drift electrons plus those whose random motions carried them toward the anode - were permitted to reach the anode, both the negative bias (relatively lower potential) of the anode and the anode sheath would disappear. There would be no need for a sheath, and the anode would be directly in contact with the plasma.
When an anode is further reduced in size, stability demands that it collect more electrons than the plasma can possibly deliver continuously to its surface. The anode must "enlarge" itself. It gives rise to a space-charge sheath, now negative, by divesting itself of a certain number of electrons and thus acquiring a positive bias. The sheath grows until its "surface" can intercept the necessary numbers of drift plus random electrons to maintain the anode current. The outer boundary of the sheath becomes the effective anode surface.
The electric field in this sheath is just the opposite of that discussed above, in which electrons were repelled. Now, instead of being repelled, even the slowest electrons coming in contact with the sheath find themselves accelerated toward the anode.
One can, of course, go on reducing the size of the anode (or, what amounts to the same thing electrically, increasing the current density in the discharge plasma). When this is done, however, the sheath at the anode must grow larger and larger, reaching farther and farther into the primary plasma in search of collectible electrons. This process is necessarily self-limiting, for as the sheath expands its electric field grows stronger and stronger. Electrons caught up in the field are accelerated to ever-greater energies. Before long, they become energetic enough to excite neutral particles they chance to collide with, and the sheath takes on a uniform glow - the skin-like anode glow already referred to. (At this point, one may imagine a relatively large stellar object built primarily of hydrogen; clothed in a uniform film of anode glow, reddish in hue, it would be classified by astronomers as a red giant star.)
If one continues the process of diminishing the size of an anode, a point is reached where ionization of neutral matter sets in. Particles are no longer merely excited by having electrons bumped to higher orbits but actually are stripped of one or more electrons in collisions. When ionization becomes appreciable, the sheath itself breaks down, and a new mode of anode burning is established.
Immediately prior to breakdown, the sheath is a faintly glowing skin over the anode surface. Then, suddenly, at one or more points of intensified activity, little tufts of secondary plasma spring into being; the mildly luminous sheath gives birth to nodules of highly luminous plasma, each of them densely populated with positive ions and free electrons that were not there an instant earlier.
Now, at least within each tuft, there is an abundance of electrons available for collection by the anode. In fact, so abundant are these free negative charges within each tuft that a repellant sheath forms between it and the anode surface to limit the flow of charge into the anode. As before, just enough electrons are collected to satisfy the requirements of the controlling discharge. The total flow of negative charge to the anode, of course, includes electrons arriving through untufted regions of the anode glow, as well as those delivered by the tufts.
Since tufting takes place within a pre-existing region of anode glow (a sheath), it increases the area of contact between the glow and the outer plasma only slightly, if at all. Thus the increase in current to the anode cannot result from capturing a greater number of electrons from the primary plasma; all collectible plasma electrons were being drawn to the anode before tufting set in. Yet, for stability, the electric current across the plasma-sheath boundary must equal the discharge drift current and the anode current. This problem, too, is neatly solved by the tufting process.
The breakdown that yields electrons deliverable to the anode also yields positive ions that can be driven in the opposite direction. Indeed, plasma stability within each tuft requires that the positive charge left behind by each liberated electron entering the anode be carried off by an ion leaving the tuft in the direction of the primary plasma. (And, to be sure, a steady supply of positive ions is essential to outer-plasma stability, too, since the drift motions of these particles carry them continuously away from the anode.)
As already noted, the random motions of free electrons in a discharge plasma are typically much more energetic than their drift motions. Consequently, the random current of electrons to an anode generally exceeds the drift current by a considerable margin. But this is not always the case, and Langmuir emphasized that a condition often conducive to tufting is too low a ratio of random - to drift-current densities. The net effect, however, is the same as that we have been discussing: the anode, in the absence of tufting, finds itself unable to collect enough electrons to satisfy the demands of the discharge.
Langmuir noted, also, that anode-tuft formation requires a gas density great enough to assure numerous particle collisions; otherwise ionization would not be intense enough to generate the many positive ions needed to break down the negative space charge of the pre-existing anode glow.(23)
In the light of the preceding discussion, and on the assumption that photospheric granules may be of the nature of anode tufts, let us tentatively conclude that the photosphere is tufted for one or more of several possible reasons:
(We have already directed an aside to the subject of red giant stars. At somewhat of an opposite extreme are the blue giants - intensely hot objects considerably larger than our Sun. May we suppose that these blue giants, which tend to be concentrated on the central axes of our galaxy's spiral arm discharges (Bruce, 24), are so oppressed by the electrical demands of such environments that, in spite of their dimensions, they must clothe themselves tightly with extremely hot tufts?)
Langmuir also observed that when tufting takes place, although each tuft is intensely luminous due to ionization, outside the regions of intense glow conditions remain "much the same as before."(25) By analogy, then, we might interpret the darker, intergranular spaces, or "lanes," of the photosphere as remnants of a pre-breakdown anode sheath. However, as we shall see, such a conclusion does not appear entirely tenable.
In passing, let us note that nearly all students of the Sun agree that the minimum temperature in the solar atmosphere is to be found just above the photosphere and not within it or below it.(26) This is a matter we shall soon have reason to dispute.
W. P. Allis has described the tufting process in terms of laboratory procedures that invoke it - raising the anode potential with respect to the primary plasma, thus increasing the discharge current while keeping the anode surface area constant. He remarks: "However, there is a limit; as the anode potential is raised past the excitation level of the gas [in which the discharge is burning], the electrons approaching the anode have enough energy to excite the gas, and [an ordinary sheath of anode glow] forms. Then as the current is raised [still further] . . . the [anode] voltage suddenly drops. It decreases while the current increases, and a tufted anode is formed.
"A tufted anode is one on which bright spots appear at various parts of the anode. [Allis illustrates this with a photograph showing six tufts of plasma floating just above the anode surface. He points out that as the current is increased or decreased, the number of tufts also increases or decreases. He notes that the tufts always appear to arrange themselves symmetrically and attributes this to mutual repulsions among them due to their net positive charges. He reports that the tufts may be stationary, or they may sometimes move around on the anode surface.] These bright spots, which are called tufts, sometimes jump around unsteadily."(27)
The seeming repulsion between tufts, mentioned by Allis, is unlikely to be an electrical effect. The electric field surrounding each tuft is contained within a sheath at the tuft boundary, and for tufts as widely spaced as those in Allis' photograph it is difficult to conceive of sheath interactions. It seems much more probable that the symmetrical arrangements of the tufts are due to momentum effects of the positive-ion streams diverging from the tufts. Such streams would tend to clear a bit of space around each tuft and urge it to retreat some distance from each neighboring tuft. At the same time, fleeting inequalities in individual rates of ion-production or -emission might account for the unsteadiness also reported by Allis.
This same author provides us with a diagram that is helpful in seeing just what an anode tuft amounts to. The basic features of this diagram are reproduced in Figure 1, which shows schematically the distribution of electric potential from a point within the primary plasma, across the secondary plasma of the tuft, to the anode surface - an electrical cross-section through the tuft.
In the sheath that separates the primary and secondary plasmas, the voltage- (potential-) distribution curve is bent like a letter "S". An inflected curve of this kind in a potential-distribution diagram is the unmistakable mark of the double sheath. Next to the lower potential (primary) plasma, in the region where the curve is concave upward, is a sheath of negative space charge. Between this and the higher-potential (secondary) plasma of the tuft, in the region where the curve is concave downward, is a sheath of positive space charge. Thus there are two sheaths, in a sense, back-to-back. Together they provide a smooth transition between the differing electric potentials of the two plasma regions.
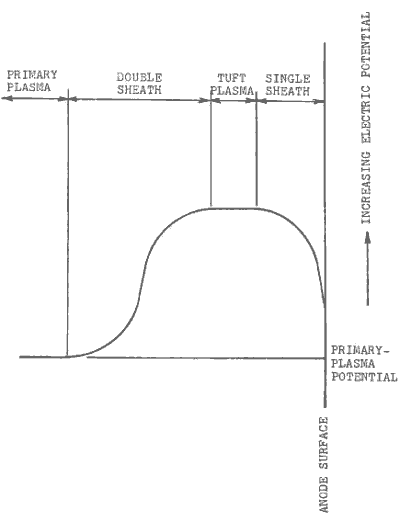 Figure 1. Potential-Distribution across an Anode Tuft (after Allis) |
(Any plateau, or horizontal section, in a potential-distribution diagram is the mark of a plasma region.) The electric field in the double sheath is strongest where the curve is steepest - at the point of inflection between the positive and the negative space-charge regions.
At the anode end of the secondary (tuft) plasma we find another positive-space-charge sheath - concave downward - that terminates on the anode surface. The diagram of Figure 1, indicates that the anode potential is rather higher than that of the primary plasma (and lower than that of the secondary plasma), but this is not necessarily the case; when ionization is strong in a tuft, the need of the anode to limit the influx of electrons may well depress its potential below that of the primary plasma.
In a much-cited, classical review paper of 1929,(28) Langmuir demonstrated that a double sheath is stable only when the current densities of the positive-ion and electron flows across it are properly related. The ratio of the electron current into the tuft to the positive-ion current out of the tuft must equal the square root of the ion mass divided by the electron mass, which is to say:
(electron current/ion current)² = ion mass/electron mass.
In deriving this expression, Langmuir assumed that the electric field vanishes on both sides of the double sheath, which is another way of saying that the sheath separates two regions of high conductivity - two plasmas - at different electric potentials. In a diagram such as that of Figure 1, as already suggested, the absence of an electric field is indicated by any horizontal run of the curve.
Allis points out that Langmuir's stability criterion is satisfied, for all practical purposes, when the tuft density divided by the primary plasma density is approximately the square root of the ratio of temperatures between incoming electrons and outgoing positive ions. He writes: "Thus tufted anodes can exist only when the electron and ion temperatures are different. They arise from the fact that the electrons are hotter than the ions, so that there is a fixed step in density across the sheath that maintains the required current ratio. . . ."(29)
This approximation, however, is unlikely to be of help in evaluating the present hypothesis, since it was never intended for use outside the laboratory. In a real atmosphere, such as that of the Sun, gravity comes into play and tends to produce vast changes in density with changes in altitude. In the solar atmosphere, furthermore, complications arise from the fact that strong magnetic fields often are present - fields capable of moving or limiting the movements of ionized gases. Eddy remarks, on the basis of Skylab findings, that "in a layer about 5000 km thick between the 6000 K photosphere and the corona drastic changes occur: the electron temperature increases by a factor of 300, density falls through eight orders of magnitude, radiative and thermodynamic equilibrium break down, and the solar plasma falls under the control of the Sun's magnetic fields".(30)
So it would be in all likelihood futile to try to test our hypothesis with Allis' rule of thumb. Langmuir's criterion, on the other hand, should be of general utility, based as it is on purely electrical requirements.
Let us now consider a rather fundamental difference between the postulated solar discharge and a laboratory discharge in which small scale anode tufts might bloom. We have suggested that an important function of the ionization process inside anode tufts is the production of positive ions to amplify the electric current across the plasma sheath boundary. The process presupposes that neutral atoms and molecules are present to become ionized. Where do they come from?
For the laboratory discharge, which is typically fired up inside a sealed vessel, there is only one answer: The neutral atoms are present in the discharge medium itself - in the plasma. The medium must harbor an abundance of neutrals, and their random motions must deliver enough of them to the vicinity of the anode to sustain the ionization processes going on in the tufts.
On the other hand, for the postulated solar discharge this cannot be the answer. The primary plasma in this case - the solar corona - is a fully ionized gas; essentially all its resident particles are already products of ionization, and its positive ions are for the most part protons, the nuclei of hydrogen atoms, certainly not subject to further ionization. There is little, if any, ionizable matter present in this plasma anywhere near the Sun.
Of course, the source of neutral atoms for photospheric granules is no mystery. The Sun itself is a ball of gas, and no one questions that granules must be loaded with neutral hydrogen drawn from the main body of the Sun.(31)
So there is a pronounced difference in geometry between supply lines feeding un-ionized gases to laboratory anode tufts and to photospheric granules. For solid-metal, man-made anodes, such gases must flow to the base of each tuft across the anode surface, approaching from all sides, and then must be drawn into the tuft through the flattened face that it presents to the anode. Actually, the need for each tuft to collect neutral matter from all directions may contribute to the symmetrical spacings tentatively laid to "mutual repulsions" by Allis. On the Sun, where such a round-about approach by neutral matter is unnecessary, we might expect granules to close their ranks, if only to prevent the escape of gases except as processed through granules.*
[*Footnote: Electric-arc lamps that practically duplicate photospheric radiation are contrived so that ionizable gases are emitted by or through porous discharge anodes.]
Since un-ionized gases presumably are abundant everywhere on the solar globe just below the photosphere, and since any appreciable leakage of neutral matter could have a disruptive effect on the postulated electric discharge,(32) we might reasonably look for granules of the anode-tuft type to cover as much of the Sun as possible. And, just so. We find photospheric granules so closely packed as to crowd and distort one another, taking on shapes that are more blocky than "semispherical." Estimates vary even today, but it seems certain that granules occupy at least two-thirds of the total surface area of the Sun (33)
If granules are anode tufts that are amenable to tight packing, could we not expect them to merge and form a continuous envelope in which ionization could proceed smoothly with no possibility of neutral-gas leakage?
This seems out of the question, for the Sun must also supply electrons to maintain the external plasma. Langmuir's stability criterion for the double sheath requires that dozens and dozens of electrons from the primary plasma (corona) enter the sheath for each positive ion that leaves it in the opposite direction. In a medium of pure hydrogen, this disparity in numbers must be about 43 to 1, and in any other kind of medium it must be even greater. Since the corona is fully ionized, or practically so, it contains free electrons in great abundance, but not so many as to constitute an endless supply. Were 43 (or more) plasma electrons to be lost to the photosphere for each positive ion given up, the essential quasi-neutrality of the primary plasma would rather quickly be destroyed.
Nor can we look to electrons arriving from the outer regions of the postulated discharge to balance such losses. Though these primary electrons presumably deliver all the energy radiated by the Sun,(34) they are few in number; their collective potency is due largely to their individually high energies.
So we must assume that the Sun itself supplies most of the free electrons required to maintain neutrality in the primary plasma. The emission of electrons by anodes otherwise bent on collecting them is a known phenomenon,(35) and we need not be overly concerned that the idea at first seems contradictory. Recognizing the abilities of electric discharges to adapt to or compromise with prevailing conditions, we may be sure that if the Sun found a need to recycle a few hard-won electrons to win some more, it would hasten to do so.
The anode-tuft explanation for photospheric granules leaves only the dark lanes between granules as channels through which electrons might be expelled from the Sun. Available knowledge of these regions does not rule out this possibility.
Observations of Fraunhofer lines - spectroscopic absorption features of the photosphere - strongly suggest that both neutral atoms and positive ions drift downward between granules.(36) This is generally interpreted as evidence of descending bulk-gas motion and as support for the convection theory of the photosphere. But if the motions of the positive ions were electrically induced, as by an anode (solar-body) potential lower than that of the primary plasma, the accompanying drift of neutral atoms could be laid to electric wind effects(37) - a transfer of momentum from field-accelerated ions to neutral members of the bulk medium. And electrons, of course, would be induced to ascend by the same forces that urged the positive ions downward.
The same Fraunhofer lines are much broadened in the dark spaces between granules. Conventionally this is attributed to turbulence in the medium, but to turbulence that is unaccountably more violent in these cooler regions than in the granules themselves.(38) It seems quite possible, however, that the observed line-broadening arises not from turbulence but from the emission of radiation in an electric field - the Stark effect.
Fraunhofer lines produced elsewhere in the photosphere show many peculiarities that have defied explanation in terms of conventionally proposed photospheric models.(39) Some lines increase in intensity to a maximum near 70 degrees from the center of the Sun's disk, then decrease again toward the limb, or the edge of the disk. A "curious phenomenon" is that lines from the extreme limb, presumably produced higher in the atmosphere than those observed near the center of the disk, are as broad as those from the center; indeed, faint and medium-intensity lines generally become broader toward the limb. Lines of light atoms are broader than those of heavy atoms.
Zirin remarks: "The problem of the production of the Fraunhofer lines is so complicated . . . that attempts to predict the profiles from model atmospheres have ended in total failure."(40) Perhaps the problem stems from limiting one's horizons with concepts of model "atmospheres".
We might suggest that a profitable approach to the study of the Fraunhofer lines would be through a model built along lines suggested here - a single-sheath substructure emitting electrons and capturing positive ions and neutrals wherever it can between superstructure anode tufts whose electrical cross-sections approximate that of Figure 1. On such a model, line-formation appropriate to fully thermalized particle motions could be expected only in granule interiors. Elsewhere, Stark line-broadenings (splittings) would be the rule, more pronounced in the higher regions visible in depth toward the limb, and generally more pronounced for light atoms than for heavy atoms.
Consider the spectrographic evidence pertaining to granules. Blue shifts in the wavelengths of granule Fraunhofer lines - Doppler effects indicating motion toward the observer, or upward - have been apparent for many years. Again, the conventional interpretation has it that this supports the idea of convection. But the inferred velocities - less than 0.5 kilometer per second - are "surprisingly small".(41) Some investigators have seen fit to "correct" such findings, arbitrarily increasing them by factors of four or so to values more in keeping with observed "turbulence". To this procedure, however, Zirin addresses some choice words: "Although there is nothing wrong with introducing such a finagle factor to patch up the shortcomings of our photospheric theory, it is going a bit too far to consider this an experimental determination of granule velocities, particularly when it disagrees with direct measurements."(42)
The velocities actually indicated by the blue shifts, if interpreted in terms not of bulk-gas convection but of electrically accelerated positive-ion motions and momentum transfer to neutral particles in a space-charge sheath, are not at all surprising. As before, the Fraunhofer-line information does not exclude the possibility that free electrons are flowing into each granule across the same sheath. And again the Stark effect could explain the observed line-broadenings.
Consider now the "temperature minimum" supposedly to be found immediately above the bright photosphere. Our present hypothesis suggests that a decrease in atmospheric energy density at this level is more imaginary than real.
The accepted treatment of the evidence is far from satisfying. To simplify matters, we shall bypass all the detailed arguments and calculations and simply quote another remark by Zirin: "The minimum is apparently reached near the edge of the white light disk (which we set as the zero point of the height scale), where the temperature is between 4000° and 4500°. It is only reasonable for the temperature to be lowest where most of the energy is escaping."(43)
The latter statement may well be true, but most of the energy put out by the Sun is escaping precisely where the photosphere is brightest - in the granules, where the temperature is more like 6000°. It follows that there is little reason to look for a markedly lower temperature some hundreds of kilometers above this level, especially considering that at still higher levels temperatures reach values far above that of the photosphere. No reason, that is, except that spectrograms seem to tell us that a temperature minimum exists.
Can the evidence be denied? The anode-tuft granule model (see again, Figure 1 ) suggests that it can, or that its accepted interpretation can be denied. Particles crossing the double sheath at the outer boundary of each tuft must be at least partially de-thermalized by the strong electric field in the central part of the sheath, quite conceivably de-thermalized to such degrees that their spectra become unreliable evidence of their actual energies.
Since only positive ions and neutral atoms give rise to the Fraunhofer lines and thence to model atmospheres, let us concentrate on what may happen to these particles in the sheath. To start with, we might recognize that positive ions come under the influence of the sheath electric field only if their random motions in the tuft plasma chance to carry them to the sheath. This means that capture by the field is selective, in that only ions with initial motions or components of motion out of the plasma can be involved. Having entered the sheath, such chosen ions are accelerated by electrical forces acting outward, perpendicular to the tuft boundaries. The predictable result is a certain ordering of velocities already once-selected for their favorable directions; the accelerations of all in line with sheath fields can only tend to align the velocities of all. Components of velocity at right angles to the field, even for neutral atoms dragged along by the positive ions, may well be damped as a result of collisions.
An external observer seeking to read the temperature of the gas in this region would conclude that it is lower than that of the granule background, although in fact the concept of gas, or medium, temperature would be quite inapplicable to the de-thermalized motions under observation. On the other hand, the actual energy density of this "cool" matter would be higher than that of the granule background.
The positive ions, accelerated electrically, and to some degree the neutral atoms propelled in the same directions by momentum transfer, must move faster and faster with increasing distance from the tuft plasma. Kinetic energies will increase as long as these particles remain subject to the sheath field, except perhaps as encounters with incoming electrons might tend to dissipate those energies. In any case, particle energies must remain irresolvable in terms of gas temperature until all motions once more become fully randomized, or thermalized.
We may say, then, that the concept of temperature as a physical quality of a medium is inappropriate to the solar atmosphere anywhere inside space-charge sheaths. On this basis, any attempt to specify temperatures for most of the region between the brightest depths of the photosphere and the nearest overlying region of thermalized plasma is foredoomed to frustration and failure. (Indeed, frustration has been the hallmark of decades of efforts by solar physicists to fathom the thermal characteristics of the chromosphere - precisely the region in question.)
In the frame of the electrical-sun hypothesis, the first true plasma we come to above the photosphere is the solar corona. From a base variously estimated to lie 2000 to 5000 kilometers above the "temperature minimum,"(44) the corona extends through interplanetary space to unknown distances from the Sun. Below the corona and above the photosphere is the chromosphere, a region whose reddish glow shines forth during those brief moments when the bright face of the Sun is hidden by the Moon during total solar eclipses. This lesser glow, its character as an envelope containing the photosphere, and even its refusal to reveal its "temperature" - all these suggest that this is a true anode glow, and that we may be on the right track in classifying photospheric granules as anode tufts.
From the earlier discussion we may infer that the seeming temperature minimum above the photosphere marks the beginning of the concave-upward wing of the double-sheath curve of Figure 1. Here the electric field is at its most intense, and here (or perhaps a bit higher in the atmosphere) the regimentation of positive-ion velocities should be most pronounced. The entire chromosphere, therefore, must be a region of negative space charge - another quality typical of an anode-glow region.
Of course, the chromosphere is not exactly the quiescent envelope it appears to be in eclipse photographs. In its own ways, it is even more complex than the tufted photosphere. Its lower regions are ravaged ceaselessly by effects too numerous and too complicated to discuss here. It is shot through with enormous, though short-lived, jets, called spicules. Eruptive prominences decorate the chromosphere, and explosive solar flares shatter it locally. All these fascinating events that take place above the photosphere perhaps attest to hundreds of second-order difficulties related to the maintenance of a stable discharge.
In passing, let us note that our earlier conclusion that the Sun must continually replenish the supply of electrons in the outer plasma (corona) seems thwarted by the present requirement that electrons be accelerated sunward in the chromosphere. But maybe the Sun recognized this paradox long ago and came to its own rescue with the spicules. These monumental jets, hundreds of kilometers in diameter, towering thousands of kilometers into the lower corona,(45) belie their rather belittling name. They apparently spew electrons and ions alike into the corona far beyond the tops of their luminous stacks.(46)
Getting back to the more prosaic photosphere, we must yet inquire as to the comings and goings of the granules. Can such short lives be squared with the anode-tuft hypothesis?
In seeking an answer to this question, suppose we pursue some further consequences of Langmuir's criterion for double-sheath stability. We recall that many dozens of electrons must pass inward across such a sheath for every positive ion that passes outward. As mentioned earlier, in a medium of pure hydrogen this ratio amounts to about 43 electrons to each positive ion (proton). It is quite conceivable, of course, that the current of 43 incoming electrons and one outgoing proton could be balanced by an outflow of 44 electrons into the anode.
But the solar gas is not pure hydrogen. It contains many "impurities," most of them atoms more easily ionized than hydrogen, and all of them in the very nature of things more massive than hydrogen. Consider just one impurity atom - say, an iron atom with a mass about 56 times that of a hydrogen atom. When this atom becomes singly ionized (when it loses one electron) and its motions carry it to the sheath boundary, it must be accelerated and thrown out of the tuft along with numerous proton companions. Langmuir's criterion requires, however, that in this event about 323 primary-plasma electrons must cross the sheath in the opposite direction.
This in itself might not be too upsetting to the electrical balance in the tuft; we may easily imagine an anode demand such that all electrons drawn in to satisfy sheath-stability needs would still be balanced by an equal number (plus one for each departing positive ion) withdrawn to the anode. But the very presence of impurity atoms more easily ionizable than hydrogen means that relatively more of them will be ionized. In turn, the plasma will become relatively overpopulated with the lower-energy electrons released in such "easy" ionizations, and this can tend to clog the works.
Another look at Figure 1 reminds us that electrons reaching the anode from the tuft plasma do so only after passing through a sheath that tends to slow them down and send them back to the tuft; the electric field in this sheath tends to send positive ions to the anode, and indeed many of them produced in each tuft must find their way to the anode, where they are undoubtedly de-ionized and restored to neutral-atom status. Only electrons with energies in excess of a certain minimum value can make it across the anode sheath.
The overall configuration of the potential-distribution curve of Figure 1 tells us that a tuft is, in a sense, a trap in which electrons of lower energies must tend to accumulate. To the degree that this happens, the negative space charge within the tuft must increase with the passage of time, and the electric potential of the tuft plasma must decrease with respect to that of the primary plasma. There is a measure of self-correction in this process, in that a lowering of the barrier in the anode sheath must permit a few more low-energy electrons to reach the anode. But it is easy to see that this cannot reverse the process. Plasma potential in the tuft must eventually drop to such an extent that the tuft is totally disabled. Energies imparted to incoming electrons by the collapsing double sheath grow feebler. De-ionization sets in like a cancerous disease, and the light of the tuft begins to fade. The once-brilliant blob of plasma simply "goes away".
An analogous process of space-charge fouling has been harnessed in the development of fast Geiger-Müller counters for the detection of radioactivity and other sources of ionizing radiation.(47) Llewellyn-Jones cites similar electronic behavior as responsible in general for the dimming of "dark-spaces" - the less-luminous regions in many kinds of electric discharge.(48)
Reported splittings(49) and incipient splittings(50) of photospheric granules may also be due to the choking effects of space-charge accumulations. In structures as vast as granules, inhomogeneities are to be expected on the grounds of size alone. And if solar matter below the photosphere is in a state of unrest anything like what might be suggested by the vagaries of solar activity,(51) we may perhaps suppose that conditions conducive to granule-formation or breakup vary rapidly.
Qualitatively, at least, it would appear that the physical characteristics and the behavior of photospheric granules are responsive to explanation in terms of the anode-tuft hypothesis. The photosphere as a whole seems to add up to yet another strong indication that the Sun draws its energy not from within itself but from its cosmic environment, and that the delivery mechanism is an electric discharge embracing the entire solar system.
NOTES AND REFERENCES
1. Cf. M Minnaert, "The Photosphere," in The Sun, G. Kuiper, ed., University of Chicago Press (1953), p. 171.